Youth Risk Behavior Surveillance

Every two years, the Centers for Disease Control and Prevention conduct the Youth Risk Behavior Surveillance System (YRBSS) survey, where it takes data from high schoolers (9th through 12th grade), to analyze health patterns. We will work with a selected group of variables from a random sample of observations during one of the years the YRBSS was conducted.
Load the data
data(yrbss)
glimpse(yrbss)## Rows: 13,583
## Columns: 13
## $ age <int> 14, 14, 15, 15, 15, 15, 15, 14, 15, 15, 15...
## $ gender <chr> "female", "female", "female", "female", "f...
## $ grade <chr> "9", "9", "9", "9", "9", "9", "9", "9", "9...
## $ hispanic <chr> "not", "not", "hispanic", "not", "not", "n...
## $ race <chr> "Black or African American", "Black or Afr...
## $ height <dbl> NA, NA, 1.73, 1.60, 1.50, 1.57, 1.65, 1.88...
## $ weight <dbl> NA, NA, 84.4, 55.8, 46.7, 67.1, 131.5, 71....
## $ helmet_12m <chr> "never", "never", "never", "never", "did n...
## $ text_while_driving_30d <chr> "0", NA, "30", "0", "did not drive", "did ...
## $ physically_active_7d <int> 4, 2, 7, 0, 2, 1, 4, 4, 5, 0, 0, 0, 4, 7, ...
## $ hours_tv_per_school_day <chr> "5+", "5+", "5+", "2", "3", "5+", "5+", "5...
## $ strength_training_7d <int> 0, 0, 0, 0, 1, 0, 2, 0, 3, 0, 3, 0, 0, 7, ...
## $ school_night_hours_sleep <chr> "8", "6", "<5", "6", "9", "8", "9", "6", "...skim(yrbss)| Name | yrbss |
| Number of rows | 13583 |
| Number of columns | 13 |
| _______________________ | |
| Column type frequency: | |
| character | 8 |
| numeric | 5 |
| ________________________ | |
| Group variables | None |
Variable type: character
| skim_variable | n_missing | complete_rate | min | max | empty | n_unique | whitespace |
|---|---|---|---|---|---|---|---|
| gender | 12 | 1.00 | 4 | 6 | 0 | 2 | 0 |
| grade | 79 | 0.99 | 1 | 5 | 0 | 5 | 0 |
| hispanic | 231 | 0.98 | 3 | 8 | 0 | 2 | 0 |
| race | 2805 | 0.79 | 5 | 41 | 0 | 5 | 0 |
| helmet_12m | 311 | 0.98 | 5 | 12 | 0 | 6 | 0 |
| text_while_driving_30d | 918 | 0.93 | 1 | 13 | 0 | 8 | 0 |
| hours_tv_per_school_day | 338 | 0.98 | 1 | 12 | 0 | 7 | 0 |
| school_night_hours_sleep | 1248 | 0.91 | 1 | 3 | 0 | 7 | 0 |
Variable type: numeric
| skim_variable | n_missing | complete_rate | mean | sd | p0 | p25 | p50 | p75 | p100 | hist |
|---|---|---|---|---|---|---|---|---|---|---|
| age | 77 | 0.99 | 16.16 | 1.26 | 12.00 | 15.0 | 16.00 | 17.00 | 18.00 | <U+2581><U+2582><U+2585><U+2585><U+2587> |
| height | 1004 | 0.93 | 1.69 | 0.10 | 1.27 | 1.6 | 1.68 | 1.78 | 2.11 | <U+2581><U+2585><U+2587><U+2583><U+2581> |
| weight | 1004 | 0.93 | 67.91 | 16.90 | 29.94 | 56.2 | 64.41 | 76.20 | 180.99 | <U+2586><U+2587><U+2582><U+2581><U+2581> |
| physically_active_7d | 273 | 0.98 | 3.90 | 2.56 | 0.00 | 2.0 | 4.00 | 7.00 | 7.00 | <U+2586><U+2582><U+2585><U+2583><U+2587> |
| strength_training_7d | 1176 | 0.91 | 2.95 | 2.58 | 0.00 | 0.0 | 3.00 | 5.00 | 7.00 | <U+2587><U+2582><U+2585><U+2582><U+2585> |
Before we carry on with the analysis, we check the dataset with skimr::skim() to get a feel for missing values, summary statistics of numerical variables, and a very rough histogram. As a result, we see that the variable “race” has the most missing values (2805).
Exploratory Data Analysis
We start analyzing the weight of participants in kilograms. Using visualization and summary statistics, we describe the distribution of weights and get visibility into the missing observations for the variable “weight”
weight <- yrbss %>% #we take the dataset and assign it to "weight"
select(weight) %>% #use the select() function to choose the weight variable
filter(!is.na(weight)) %>% #we filter out the missing data
summarise(mean=mean(weight), #calculate the summary statistics of weight variable
SD=sd(weight),
median=median(weight),
min=min(weight),
max=max(weight))
# show summary statistics
weight%>%
kbl()%>%
kable_styling()| mean | SD | median | min | max |
|---|---|---|---|---|
| 67.9 | 16.9 | 64.4 | 29.9 | 181 |
ggplot(yrbss,aes(x=weight)) + #graph the density plot of weights
geom_density(fill="light blue",color="blue")+
labs(title="Distribution of weights has positive skew")+
xlab("Weight in kg")+
theme_bw()+
NULL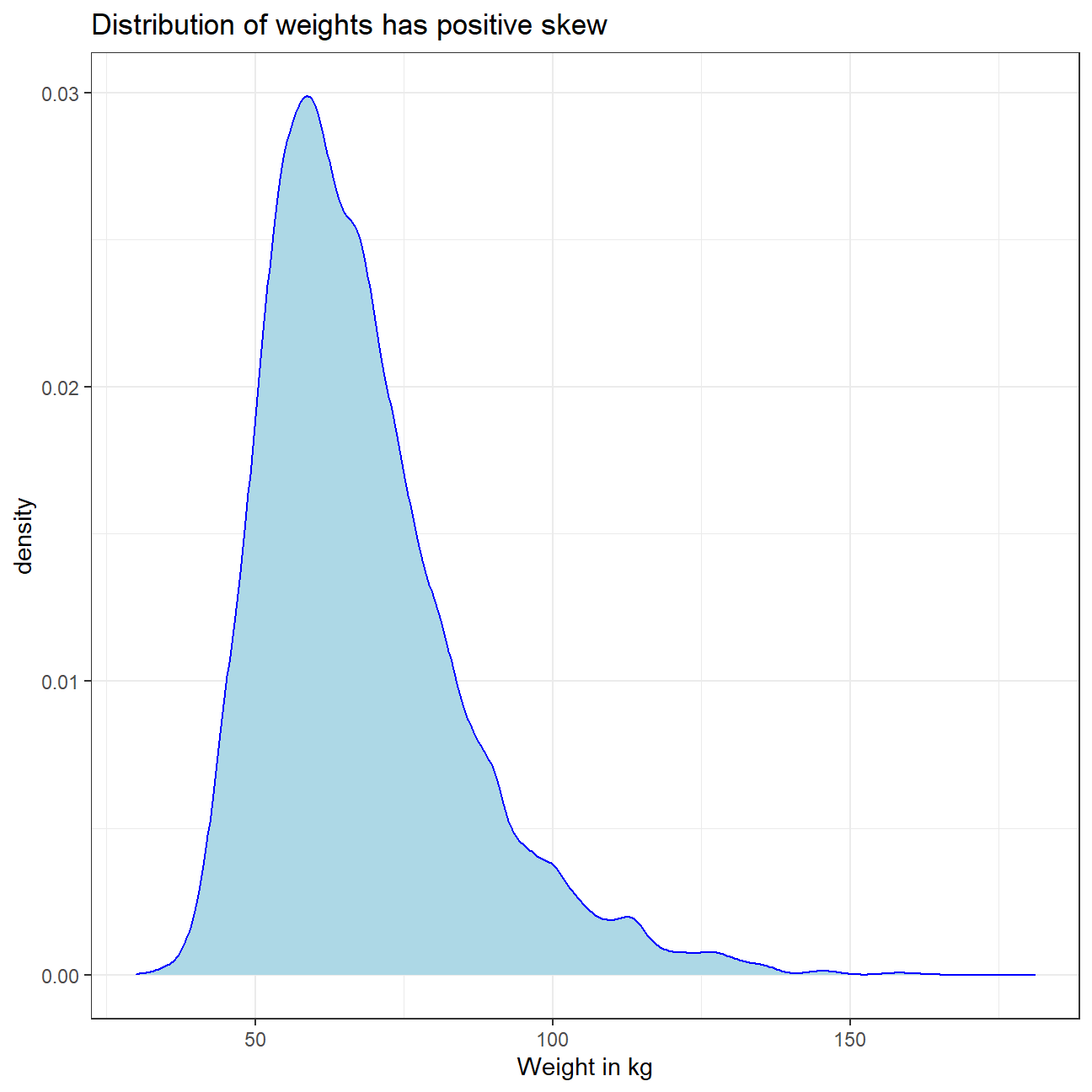
Next, consider the possible relationship between a high schooler’s weight and their physical activity. We create a new variable physical_3plus, which will be yes if they are physically active for at least 3 days a week, and no otherwise.
yrbss <- yrbss %>%
mutate(physical_3plus = ifelse(physically_active_7d >= 3, "yes", "no")) #introducing a new variable
yrbss %>% filter(!is.na(physical_3plus)) %>%#filtering out missing values for 'physical_3plus' variable
group_by(physical_3plus) %>% #grouping to calculate proportions
summarise(count = n()) %>%#counting the results
mutate(prop= count/sum(count)) #introducing and calculating proportions ## # A tibble: 2 x 3
## physical_3plus count prop
## <chr> <int> <dbl>
## 1 no 4404 0.331
## 2 yes 8906 0.669Then, we provide a 95% confidence interval for the population proportion of high schools that are NOT active 3 or more days per week, and also visualize the CI.
not_active <- yrbss %>%
specify(response = physical_3plus, success="no") %>%
generate(reps = 1000, type = "bootstrap") %>% #using bootsrapping to calculate confidence intervals
calculate(stat = "prop")
CI_95 <- not_active %>%
get_ci(level = 0.95, type = "percentile") #calculating 95% CI
CI_95%>%
kbl()%>%
kable_styling()| lower_ci | upper_ci |
|---|---|
| 0.323 | 0.339 |
visualize(not_active) + #plotting distribution for not_active
shade_ci(endpoints = CI_95,fill = "blue", alpha=0.2)+
geom_vline(xintercept = CI_95$lower_ci, colour = "red")+
geom_vline(xintercept = CI_95$upper_ci, colour = "red")+
theme_stata() #choosing the theme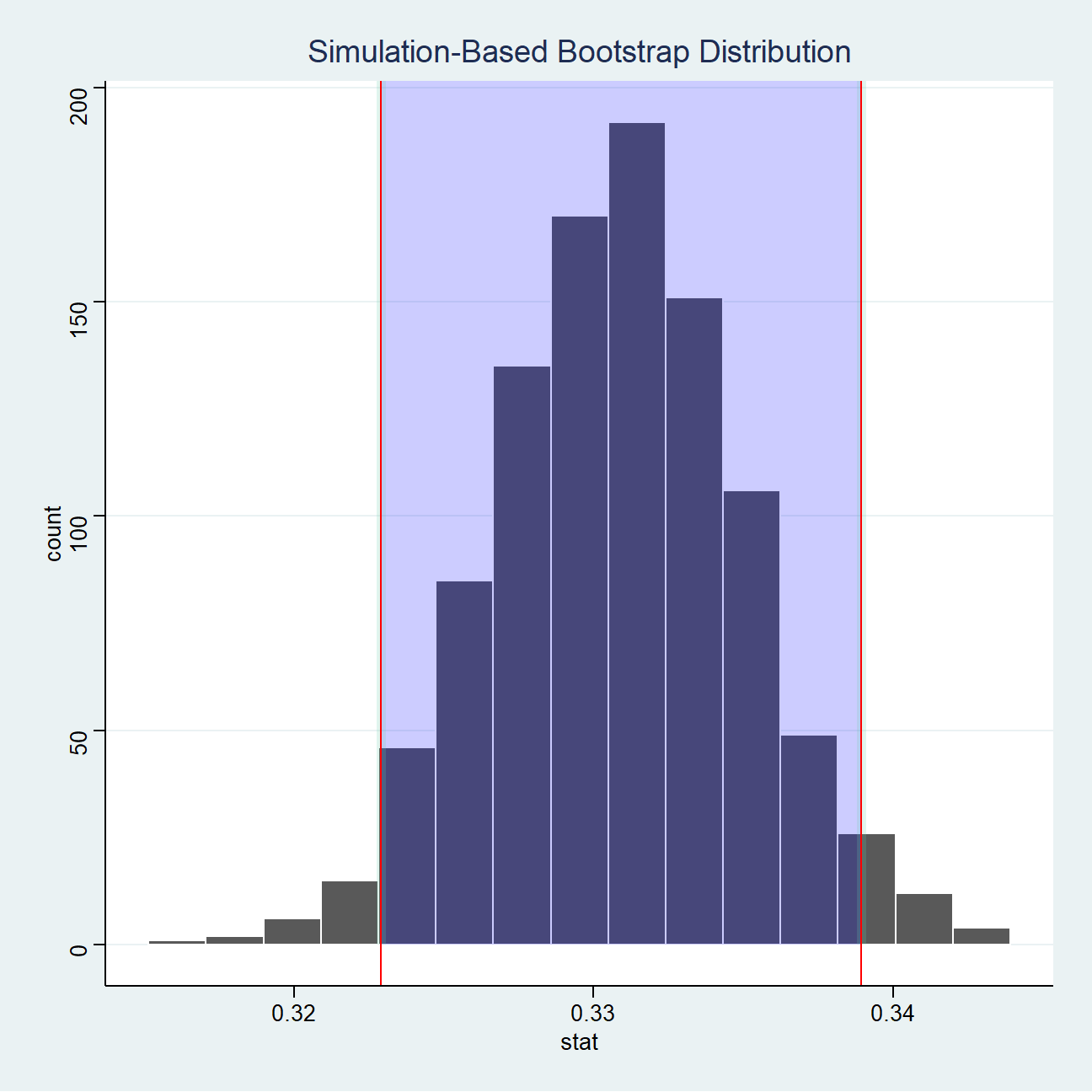
We Make a boxplot of physical_3plus vs. weight to see if there is a relationship between these two variables. We were expecting to see some relationship as phyisical activity impacts weight - more physical activity is usually expected to result in weight loss.
yrbss1<-yrbss%>%
filter(physical_3plus!="NA") #filtering out observations that have missing values of 'physical_3plus'
ggplot(yrbss1,aes(x=physical_3plus,y=weight))+
geom_boxplot(fill="light blue",color="blue")+
labs(title ="More physical activity ties to lower weight",
subtitle = "Relationship between having physical activity more than 3 days a week and weight",
x="Physically active for at least 3 days a week?",
y="Weight in kg")+
theme_bw()+
NULL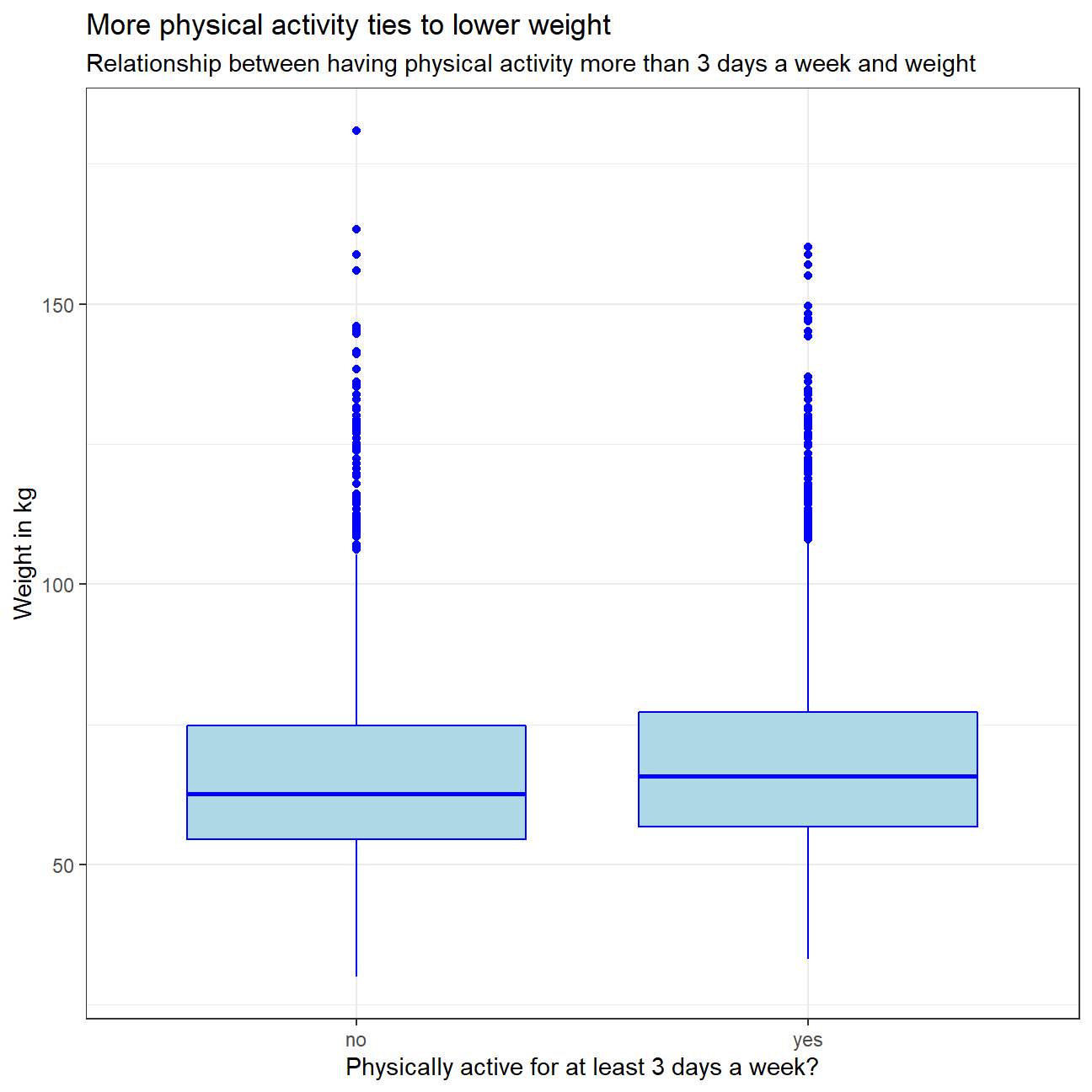
The results are partly counterintuitive, as the boxplot graph shows that the median weight of those who workout 3 or more times a week is slightly higher than the median of those who don’t. However, we have to keep in mind that in the group “No” we have data not only for those who do not work out at all, but also people who work out less than 3 times a week. A rationale for the higher median weight could be that people who work out more than 3 times a week have a goal of building more muscle vs. losing weight. Hence, higher median weight. To further explain the intuition behind it, we would need to at least split the “No” group into observations that are physically active 1-2 days a week, and those who are not active at all.
The intuitive part is, however, that working out 3 or more days eliminates the outliers who have 150+ kg weight in the other group of observations.
Confidence Interval
Boxplots show how the medians of the two distributions compare, but we can also compare the means of the distributions using either a confidence interval or a hypothesis test. Note that when we calculate the mean/SD, etc weight in these groups using the mean function, we must ignore any missing values by setting the na.rm = TRUE.
yrbss %>%
group_by(physical_3plus) %>%
filter(!is.na(physical_3plus)) %>%
summarise(mean_weight = mean(weight, na.rm = TRUE),
sd_weight = sd(weight, na.rm=TRUE),
count = n(),
se_weight = sd_weight/sqrt(count),
t_critical = qt(0.975, count-1), #calculating statistics for 95% CI
margin_of_error = t_critical * se_weight,
lower = mean_weight - t_critical * se_weight, #calculating CI
upper = mean_weight + t_critical * se_weight) # calculating CI## # A tibble: 2 x 9
## physical_3plus mean_weight sd_weight count se_weight t_critical
## <chr> <dbl> <dbl> <int> <dbl> <dbl>
## 1 no 66.7 17.6 4404 0.266 1.96
## 2 yes 68.4 16.5 8906 0.175 1.96
## # ... with 3 more variables: margin_of_error <dbl>, lower <dbl>, upper <dbl>There is an observed difference of about 1.77kg (68.44 - 66.67), and we notice that the two confidence intervals do not overlap. It seems that the difference is at least 95% statistically significant. Let us also conduct a hypothesis test.
Hypothesis test with formula
Write the null and alternative hypotheses for testing whether mean weights are different for those who exercise at least times a week and those who don’t.
t.test(weight ~ physical_3plus, data = yrbss)##
## Welch Two Sample t-test
##
## data: weight by physical_3plus
## t = -5, df = 7479, p-value = 9e-08
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## -2.42 -1.12
## sample estimates:
## mean in group no mean in group yes
## 66.7 68.4Hypothesis test with infer
Next, we will introduce a new function, hypothesize, that falls into the infer workflow. You will use this method for conducting hypothesis tests.
But first, we need to initialize the test, which we will save as obs_diff.
H0: difference in means of students who are physically active 3 or more days a week and students who are not is equal to 0 H1: difference in means of students who are physically active 3 or more days a week and students who are not is not equal to 0
obs_diff <- yrbss %>%
specify(weight ~ physical_3plus) %>%
calculate(stat = "diff in means", order = c("yes", "no"))After you have initialized the test, we need to simulate the test on the null distribution, which we will save as null.
null_dist <- yrbss %>%
specify(weight ~ physical_3plus) %>%
hypothesize(null = "independence") %>%
generate(reps = 1000, type = "permute") %>%
calculate(stat = "diff in means", order = c("yes", "no"))We can visualize this null distribution with the following code:
ggplot(data = null_dist, aes(x = stat)) +
geom_histogram(fill="light blue",color="blue")+
labs(title="The null distribution is normal")+
theme_bw()+
NULL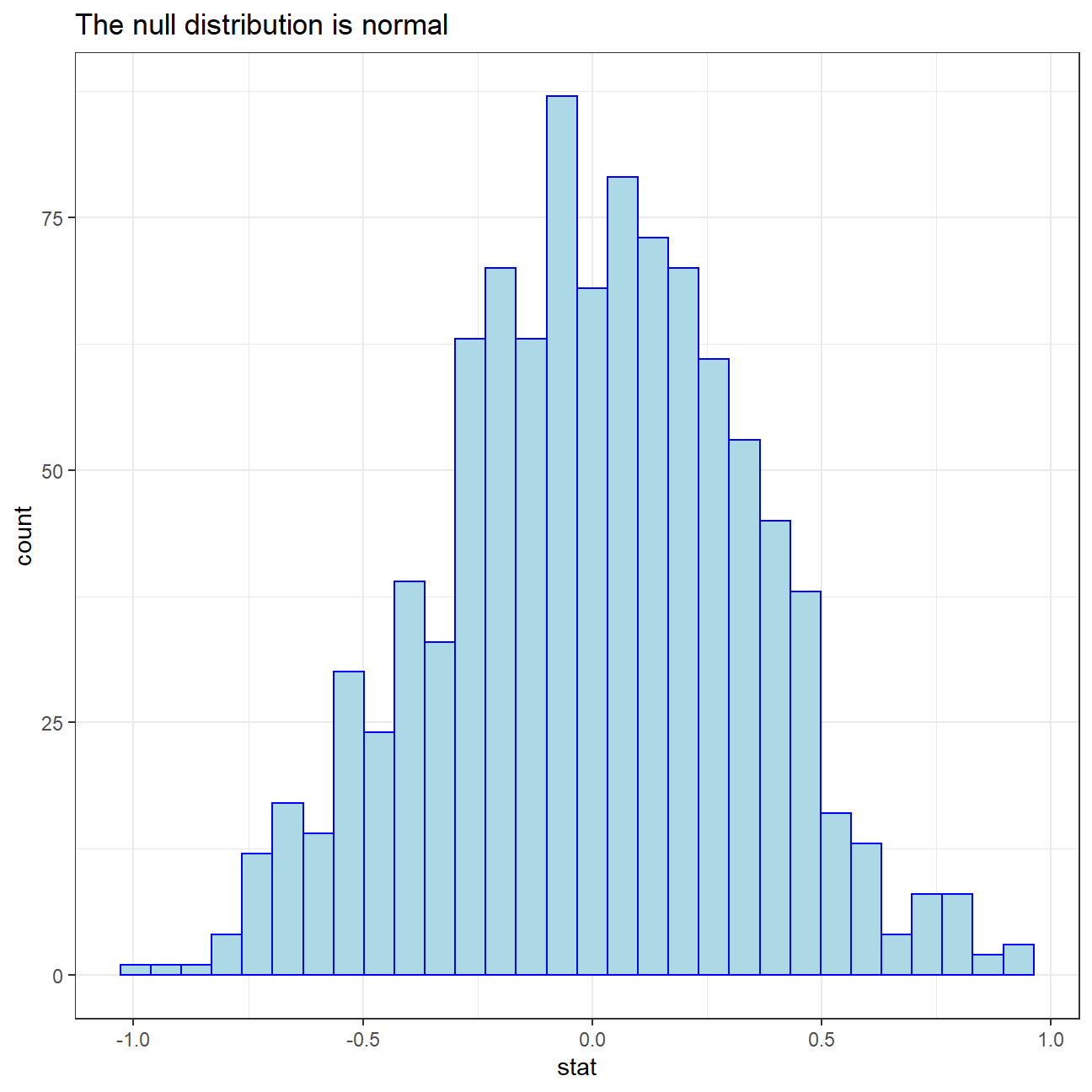
Now that the test is initialized and the null distribution formed, we can visualise to see how many of these null permutations have a difference of at least obs_stat of 1.77?
We can also calculate the p-value for the hypothesis test using the function infer::get_p_value().
null_dist %>% visualize() +
shade_p_value(obs_stat = obs_diff, direction = "two-sided")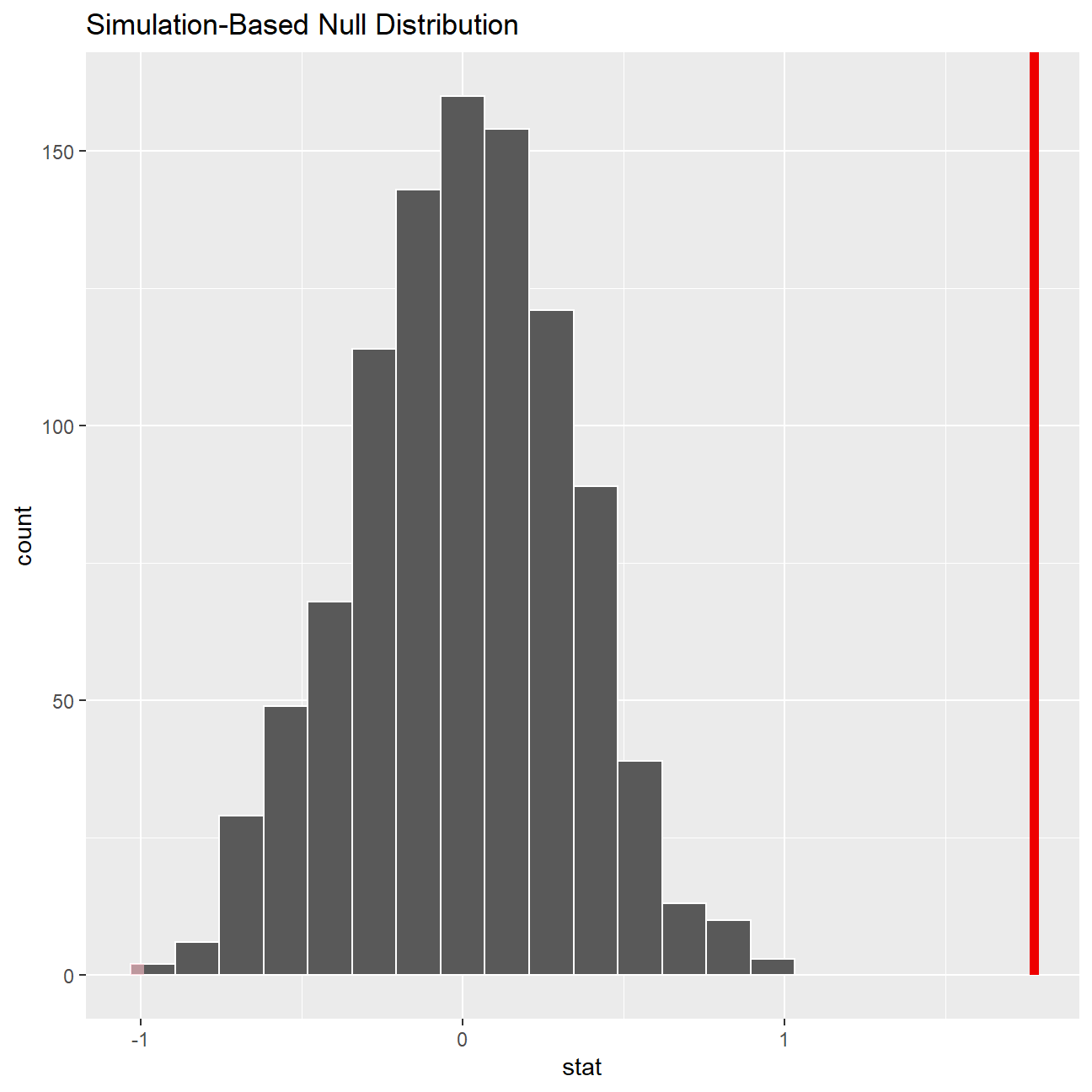
null_dist %>%
get_p_value(obs_stat = obs_diff, direction = "two_sided")## # A tibble: 1 x 1
## p_value
## <dbl>
## 1 0To sum up, we initially got the feel of the data by plotting it with boxplot and saw the difference in the two groups. To validate the difference of mean weight in the two groups, we performed hypothesis testing and as a result rejected the null hypothesis. There is enough evidence to suggest that there is statistically significant difference in the mean weight of students who are physically active 3 or more days a week and the mean weight of students who are not.